I’m in the early stages of learning Python – and by early I mean 3 days (about 5 hours total) in. My previous experience with Python was hearing people complain about (or mock) indent based scoping. To learn Python I’ve choose to work through some of the Project Euler problems. This post is specifically about Problem 18 (Find the maximum sum travelling from the top of the triangle to the base. Problem 67 is the same except that it’s dataset is significantly larger so a brute force solution will not work.
Let’s start by looking at our sample graph (this is the sample from the problem website):
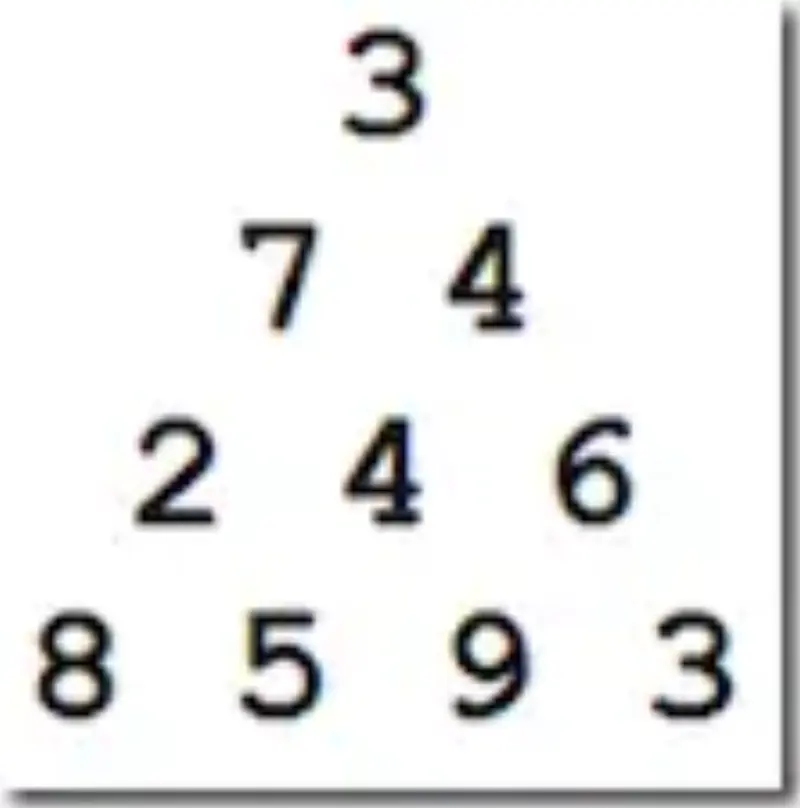
And we want to find the most expensive path from the root (3) to the bottom row (8 5 9 3).
In this example the maximum path has the value 23
On a small triangle (graph) like this we can just see the answer – but how would we do it with 16 or 100 rows (problems 18 and 67, respectively)?
We could enumerate every path – in the sample above that is 8 potential paths (the number of paths is s^(n-1) where n is the number of rows in the triangle). But in a 100 row triangle that is 2^99 paths – forget about it.
What we can do I is realize that we don’t need to know every path – we only need to the know the most expensive (largest weight) paths. With that in mind we can avoid searching any paths. Let’s talk through this.
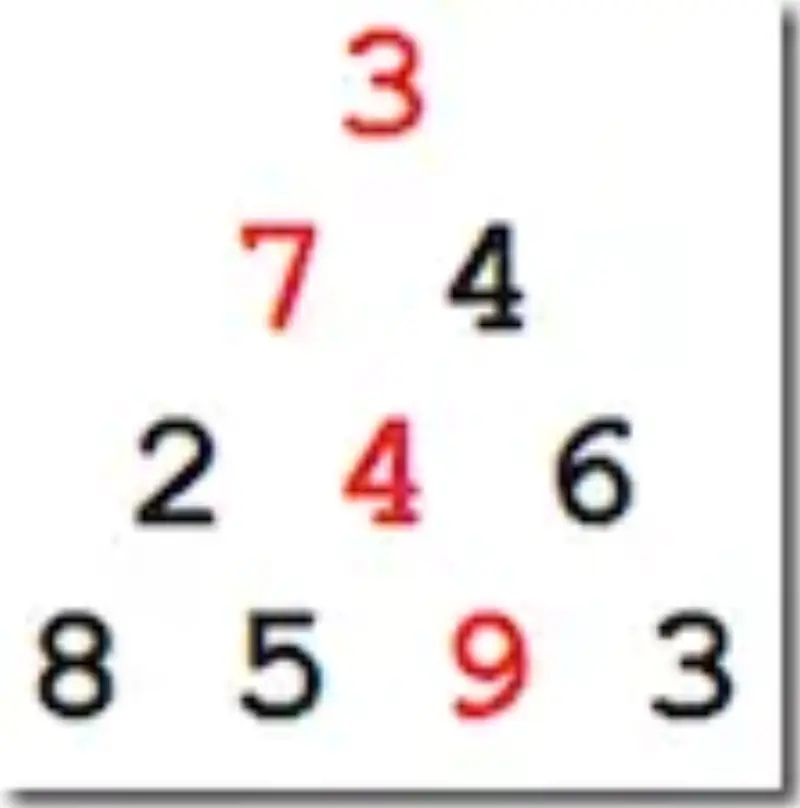
We start on the root node, 3. 3 has no parents so it’s overall weight is it’s value: 3.
On to the next row. The first node, 7, has a single parent: 3. So it’s overall weight is (7+3) = 10. The node 4 has an overall weight of (4+3) = 7. Now don’t go thinking “Ok, we can ignore 4!” – you can’t.
Now let’s step back and realize that between every connected pair of nodes there exists one path whose overall weight is greater than all the other paths (maybe there are some that are equal – but we don’t need to worry about that since it doesn’t affect the outcome). The maximal path weight for any given node depends on how many parents it has.
- No parents – the node’s value is it’s maximal path weight (this is the root node, 3)
- One parent – the node’s maximal path weight is the maximal weight of it’s parent + it’s value (e.g, 7 + 3)
- Two parents – the node’s maximal path weight is greater of it’s parent’s maximal weights + it’s value (we’ll see this in a minute)
So far we’ve seen 3 nodes. One of them had no parents (3) and two had one parent (7 and 4). So for those three nodes we know their maximal path weight. Since we know their weight we never to calculate those nodes again. So our tree can now be thought of this like this:
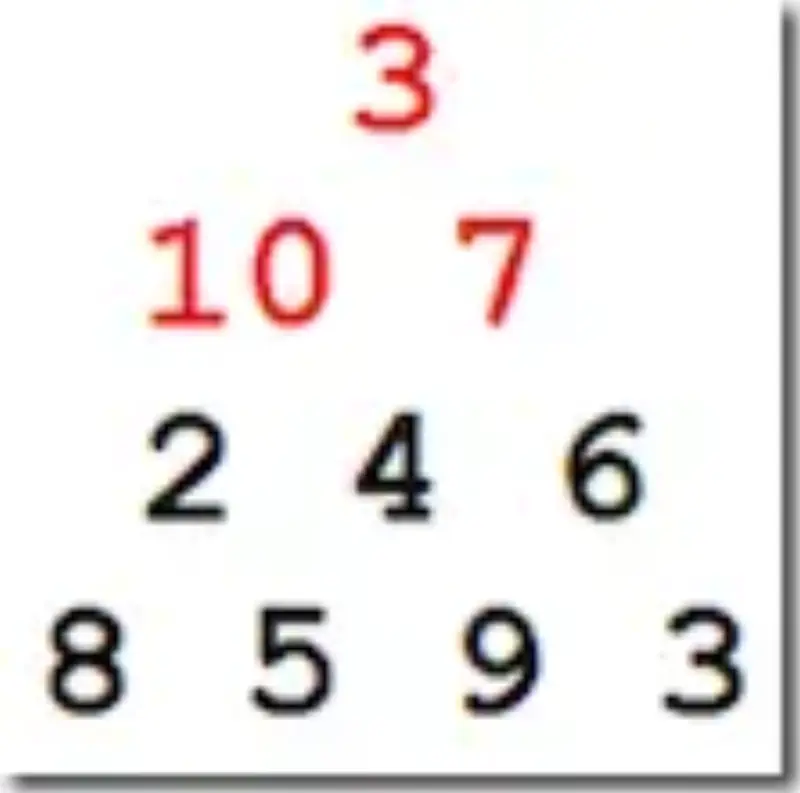
Moving on to the third row – let’s apply those maximal path rules and see the new values:
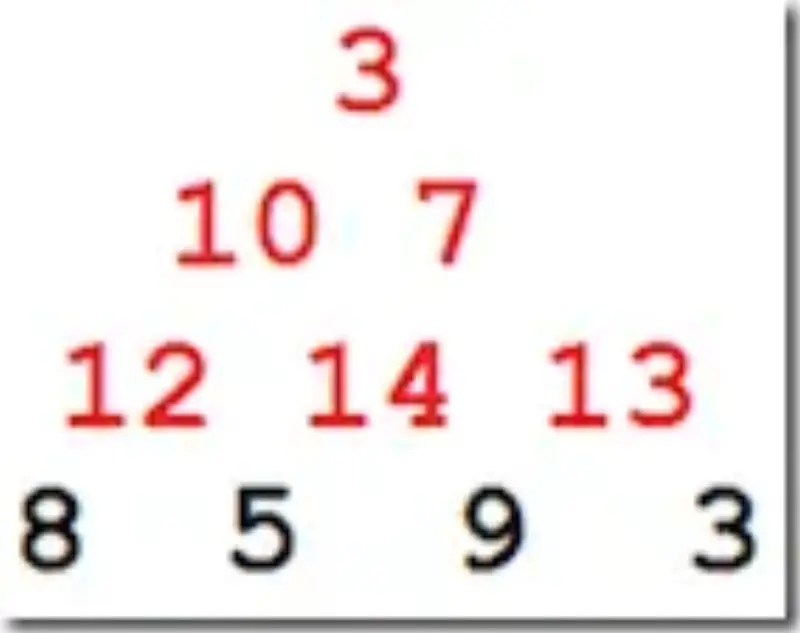
And now we can finish the third row …
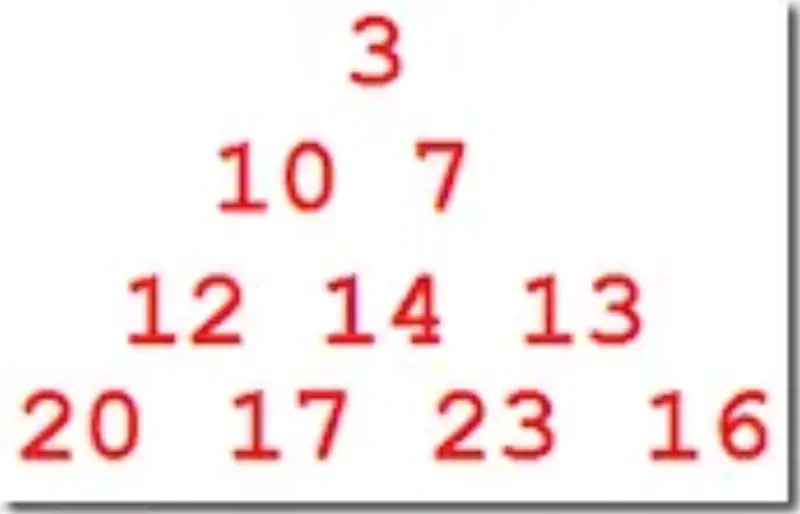
And there you have it – the maximal path value of each node is known.
So what about code?
Well – I could print the code but that would rob you of the opportunity to solve this problem on your own. My solution runs in about 30 milliseconds on the 100 row triangle – not too bad when you consider the brute force approach is estimated to take billions of years (see the explanation at the problem 67 page).